Sistema de ecuaciones lineales.
Un sistema de ecuaciones lineales o sistema de lineal,es un conjunto de ecuaciones de primer grado que deben verificarse simultáneamente.
Solución de un sistema de ecuaciones lineales.
Para hallar la solución de un sistema de ecuaciones lineales consiste en encontrar una solución común a todas las ecuaciones del sistema.
A continuación te presentaremos como resolver ecuaciones a través de los 4 métodos.
•Métodos de solución.
- Eliminación, Reducción ax±by=±c
- Igualación.
- Remplazo, Sustitución
- Gráfico (coordenadas cartesianas)
Para resolver el sistema de ecuaciones por reducción se procede así:
*Se multiplicar la primera ecuación por ( -2).
*Se suma con la segunda ecuación.
*Encontramos el valor de x.
*Se sustituye el valor encontrado en cualquiera de las ecuaciones del sistema.
El sistema anterior también se puede resolver utilizando el método de igualación,así.
*Se despeja la misma variable en las dos ecuaciones.
*Se igualan las dos ecuaciones.
*Se realizan el producto cruzado.
*Se multiplica y despeja.
*Se remplaza en cualquiera de las ecuaciones del sistema y se encuentra la otra variable.
*Se igualan las dos ecuaciones.
*Se realizan el producto cruzado.
*Se multiplica y despeja.
*Se remplaza en cualquiera de las ecuaciones del sistema y se encuentra la otra variable.
SUSTITUCIÓN Despejar cualquier variable.
Para resolver el sistema de ecuaciones por sustitución se procede,así.
*Se despeja x de la primera ecuación.
*Se sustituye esta expresión en la segunda ecuación.
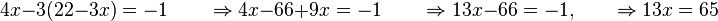
*Se sustituye esta expresión en la segunda ecuación.
*Se aplica la propiedad distributiva.
*Se determina el valor de la variable.
*Se determina el valor de la variable.
GRÁFICO y=f(x)
* La solución de un sistema de ecuaciones lineales por el método gráfico esta determinada por el punto de intersección de las dos rectas.
Los sistemas se clasifican en:
- Compatibles determinados, compatibles indeterminados e incompatibles.
Los sistemas se clasifican en:
- Compatibles determinados, compatibles indeterminados e incompatibles.

Sistema de ecuaciones
¿Sabias que? Un sistema de dos ecuaciones de primer grado con dos incógnitas, también se puede llamar sistema de ecuaciones lineales 2x2
Una Solución
|
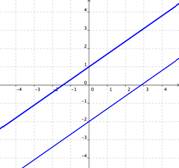
Sin Solución
|
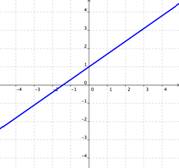
Soluciones Infinitas
|
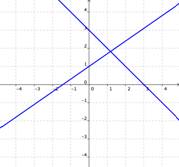 |  |  |
Si las gráficas de las ecuaciones se interceptan, entonces existe sólo una solución para las ecuaciones.
|
Si las gráficas de las ecuaciones no se interceptan, (por ejemplo, si son paralelas), entonces no existe ninguna solución para las ecuaciones.
|
Si las gráficas de las ecuaciones son la misma, entonces hay un número infinito de soluciones para las ecuaciones.
|

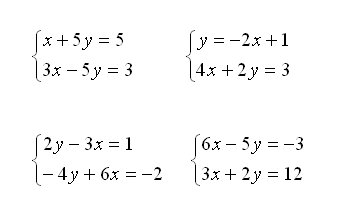


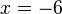
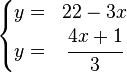


No hay comentarios:
Publicar un comentario